“Pathological Outcomes of Observational Learning”, Smith and Sorensen (Econometrica, 2000)
ORIGINAL 1996 MIT WORKING PAPER VERSION
Lowdown summary: Earlier work by Banerjee (1992) and Bikhchandani, Hirshleifer, and Welch (1992) happened up a nice model of sequential decision making where individuals with identical preferences decide upon an action from a finite menu, after seeing a private signal and all prior choices. They correctly deduced that individuals eventually herd on an action. But
- Both concluded that with positive probability, this “herd” was on a suboptimal action
- BHW highlighted another possibility of a “cascade”, where all learning stops and people ignore signals. In fact, it was merely an artifact of their multinomial signal distribution. For most common continuous signal distributions, this never arises.
Our paper develops the general theory valid for all signal distributions and two states. We also explore a fun possibility when individuals have divergent ordinal preferences.
More Extended Abstract: Informational herding may well be the most cited micro theory literature in the last thirty years. It explores how Bayes-rational individuals learn sequentially from the discrete actions of others. Ironically, hundreds or thousands of papers in this arena succumb to the problem they study. The literature started out with a bang — a claim based on a multinomial signal family that herding produces (1) cascades, (2) a positive probability of incomplete learning, and (3) an eventual “herd” of people copying one another. My early paper with Peter Sorensen proved that two these three conclusions were artifacts of the multinomial signal family. The generally true true results are actually more intriguing — for typical signal distributions, people generally never stop learning and yet herds arise — a perpetual string of identical actions. And when this signal family has unbounded likelihood ratios, learning is correct.
Unlike earlier informational herding papers, we also admit heterogeneous preferences. Not only may type-specific `herds’ eventually arise, but a new robust possibility emerges: confounded learning. Beliefs may converge to a limit point where history offers no decisive lessons for anyone, and each type’s actions forever nontrivially split between two actions.
To verify that our identified limit outcomes do arise, we exploit the Markov-martingale character of beliefs. Learning dynamics are stochastically stable near a fixed point in many Bayesian learning models like this one.
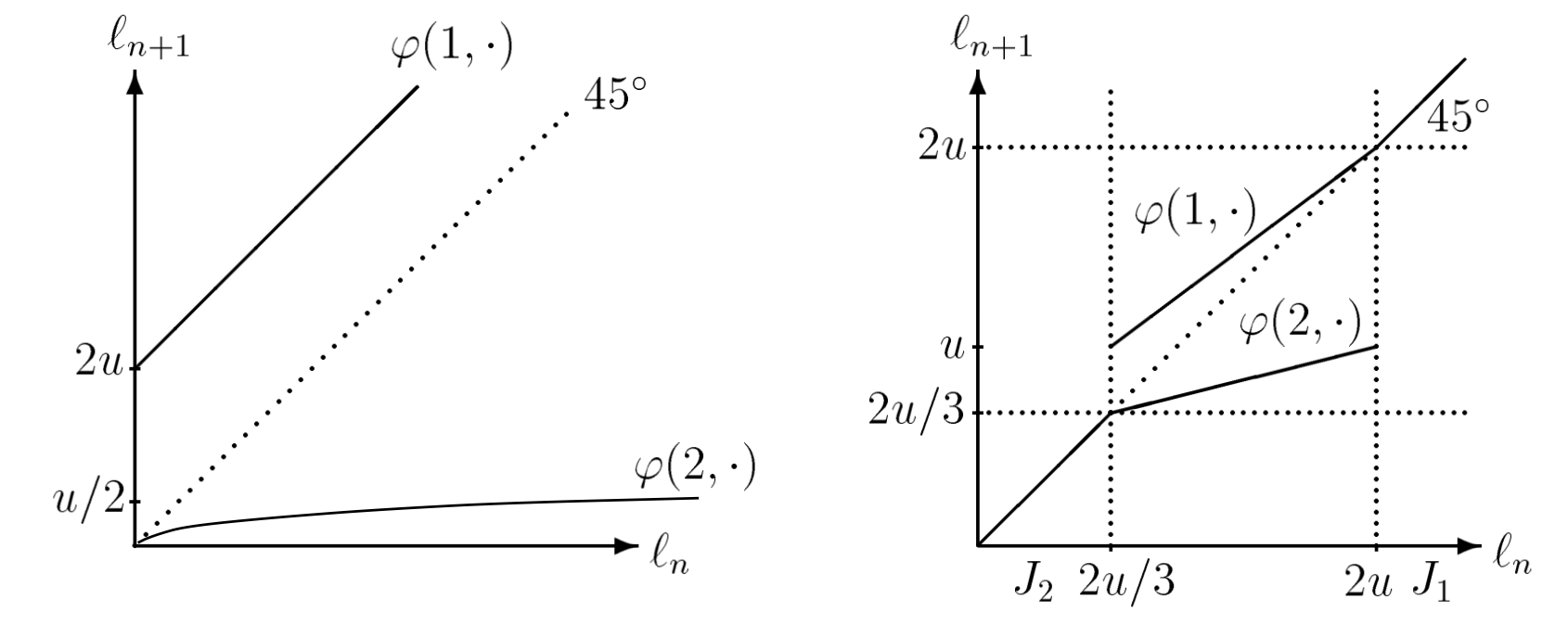
Dynamics of Social Learning
