“Optimal Electoral Timing: Exercise Wisely and You May Live Longer”, Keppo, Smith, and Davydov (Review of Economic Studies, 2008)

NOTE: I recently applied this paper’s finding in a blog post: The 50% Brexit Vote Threshold Defies Logic

PAPER SUMMARY:

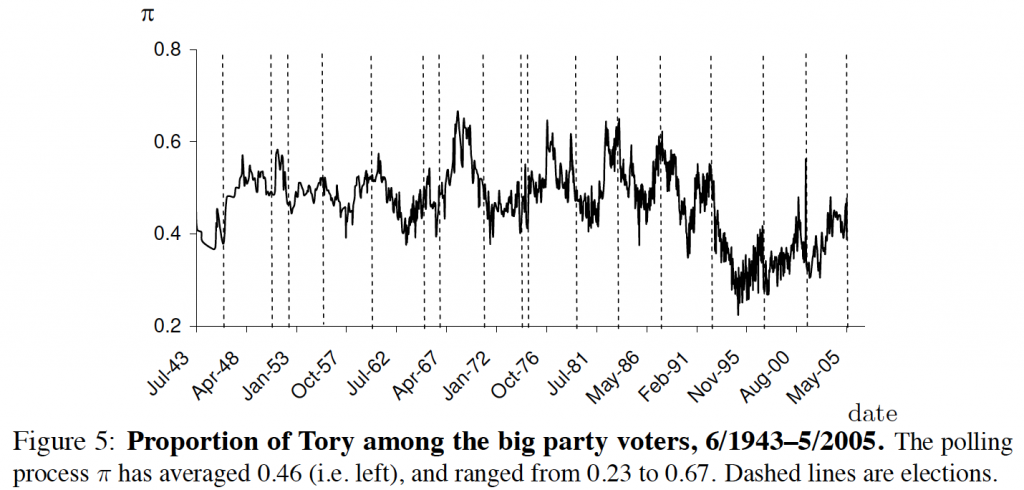
We first deduce a novel and statistically significant model of the polling process. Nate Silver is famous for his purely statistical model of the polls, say for Trump, but our model escapes his purely kitchen sink mysterious approach. We assume that the best party is hidden from all, and periodically and randomly changes according to a continuous-time Markov process. Voters have heterogeneous cardinal preferences.

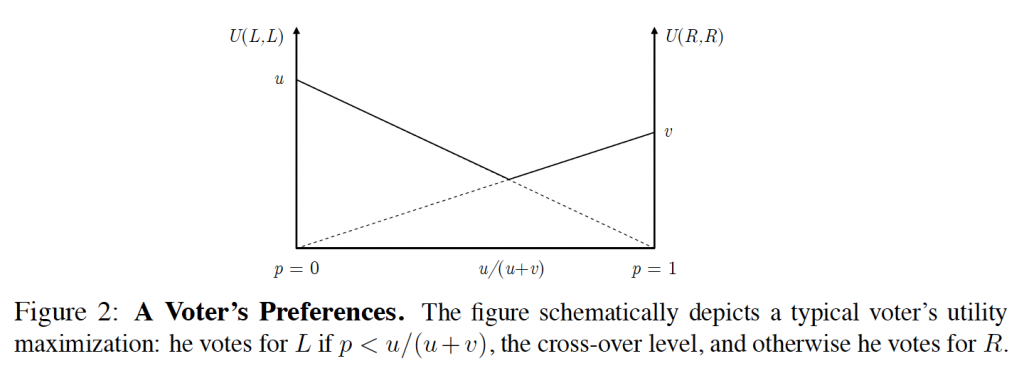Voters continuously learn over time about this unobserved Markovian state from the news media. As in finance, this is modeled as a continuous time diffusion process. The polls then are noisy reflections of voter heterogeneity, these fickle fortunes of political parties, and the continuous onslaught of media information. The result is a tractable mean-reverting stochastic process whose long-run distribution we precisely compute.

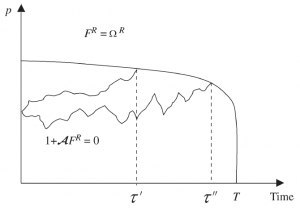
Next, the timing of elections is flexible in many countries.  We explore optimal electoral timing, modeling it as a renewable American option with interacting waiting and stopping values. The government continuously entertains a waiting value depending on its support and time left. It calls an election when its political standing first hits a non-linear stopping barrier. Since the winning government reacquires the election calling option, the stopping value is recursively defined in terms of future waiting values.

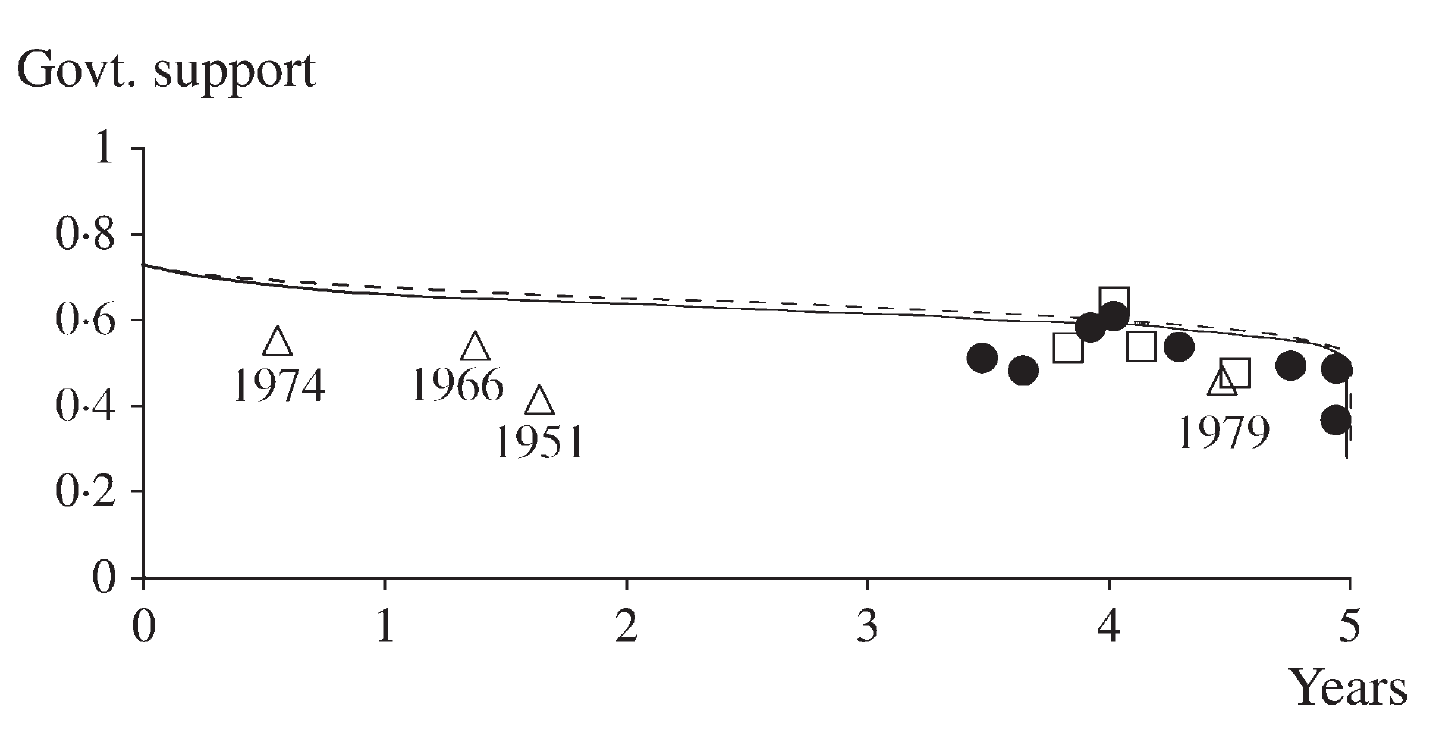
Inter alia, we show that the expected longevity is a convex, then concave, function of the support. Finally, we calibrate our model to the post-1945 Labour–Tory U.K. rivalry. Our story quite well explains when the elections were called. We also show that election options approximately double the expected time in power in the current streak.